Linear Regression cost 함수 최소화
Linear Regression cost 함수 최소화
머신러닝의 Linear Regression cost를 줄이는 방법
Hypothesis 와 Cost
H(x) = w * x + b
이게 우리가 앞서 했던 가설이었다.
그리고 Cost를 구해 주는 함수를 만들어 사용했었다.
cost = tf.reduce_mean(tf.square(y - hypothesis))
모든 손실읠 재곱을 더하고 그 총 합에서 평균의 루트값을 추출했다.
RMSE라고도 한다. - 평균 제곱근 오차
손실 줄이기
앞서 했던 minimize를 진행하면 손실이 줄어들다 일정 시점을 넘어가면 다시 증가한다.
우리는 아래와 같은 상황에서 손실이 가장 낮은 시점을 찾아야 한다.
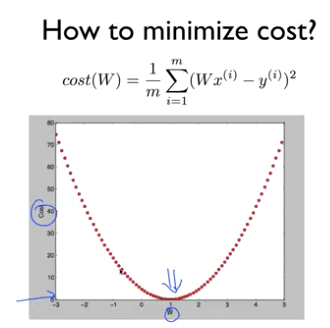
이렇게 손실을 점차 줄여 나가는 방법을 경사 하강법이라 한다.
앞선 실습에서의 가제는 w와 b를 찾는 것 이었지만, 더 많은 종류의 특성(feature)를 사용해 가장 최적의 시점을 찾아 나가야 한다.
실습
https://www.inflearn.com/course/기본적인-머신러닝-딥러닝-강좌/lecture/3381
cost를 최소화 한다는 것은 가장 손실이 적은 w,b 값을 찾는 다는 것
이번에는 더 심플하게 다시 해보자
x = [1,2,3]
y = [1,2,3]
Linear Regression Model
# Model
class LinearModel:
def __init__(self):
self.weight = tf.Variable(tf.random.normal([1]), name = 'Weight')
def __call__(self, x):
return x * self.weight
def cost(self,x , y):
return tf.reduce_mean(tf.square(y - self(x)))
학습 함수
def train(linear_model, x, y, steps, lr = 0.1):
steps_list, losses = [], []
for step in range(steps):
with tf.GradientTape() as tape:
current_loss = linear_model.cost(x, y)
lr_weight = tape.gradient(current_loss, [linear_model.weight])
linear_model.weight.assign_sub(lr * lr_weight[0])
steps_list.append(step)
losses.append(linear_model.cost(x, y).numpy())
if step % 100 == 0:
print(f'step: {step}, RMSE: {linear_model.cost(x, y)}')
plt.scatter(steps_list, losses)
동작 확인
x = [1,2,3]
y = [1,2,3]
linear_model = LinearModel()
train(linear_model, x, y, 1000, lr = 0.05)
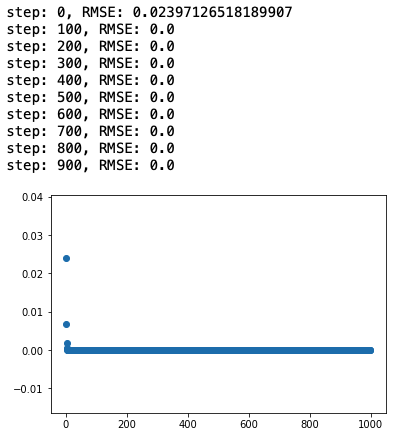
예측
value = linear_model(4)
print(linear_model.weight.numpy())
==> [1.]